RrM, выходи, давай AoPS обсудим

[Komissar]

Ну вот не понимаю я lovefest вокруг Эйопса. ИМХО, крайне несистематичный подход. Но я тебя уважаю, а ты вроде бы любишь. Расскажи, what am I missing?

[RrM]

Хм. Define "систематичный подход". И расскажи, почему он хорош? необходим? Ну в общем, почему ты считаешь "крайнюю несистематичность" заведомо отрицательным качеством?

[Komissar]

Хм. Define "систематичный подход". И расскажи, почему он хорош? необходим? Ну в общем, почему ты считаешь "крайнюю несистематичность" заведомо отрицательным качеством?

Мать, слушай, а разве не ты все время подчеркивала, что важна систематичность преподавания математики, а не bag of facts? Не пойми меня неправильно. Нет, не считаю "сиськемасиськный" подход таким уж необходимым. Сильно талантливый ребенок, аки Ломоносов, сам найдет Периодическую систему среди разрозненных фактов. Впрочем... то, кажется, был не Ломоносов... Не важно.

Но сиськемасиськный подход, ты, наверное, согласишься - эффективен, имею в виду получение знания за минимальное (с поправкой на способности ребенка) время.

Задам конкретный вопрос. Знаешь ли ты онлайн программы от BYU (рассадник мормонства)? Если да, то считаешь ли ты, что лучше сначала пройти BYU для сисьмасисьтости, а уже потом порешать задачки из аопс для практики и мозговыверта?

[Murka_]

А почему вы переживаете? У вас дети вроде уже не в школе. По теме, мне АОПС нравится. Не вижу, что плохого.

[Komissar]

А почему вы переживаете? У вас дети вроде уже не в школе. По теме, мне АОПС нравится. Не вижу, что плохого.

Мы с супругой фанаты вопросов образования и поступления.

[DropAndDrag]

Ну вот не понимаю я lovefest вокруг Эйопса. ИМХО, крайне несистематичный подход. Но я тебя уважаю, а ты вроде бы любишь. Расскажи, what am I missing?

а что-то появилось или есть лучше?

[Komissar]

Ну вот is.byu.edu в качестве первого знакомства мне показался систематичнее.

[krem]

Ну вот не понимаю я lovefest вокруг Эйопса. ИМХО, крайне несистематичный подход. Но я тебя уважаю, а ты вроде бы любишь. Расскажи, what am I missing?

а что-то появилось или есть лучше?

Наши двое ходили на тестирование а АоПС, тестирование очень понравилось, вопросы не стандартные.
Не понравилась цена и количество учеников в классе.

Решили остаться с онлайн тютором.

Но бизнес у них идёт хорошо, все классы заняты.

[Sergunka]

Не понравилась цена и количество учеников в классе.

А сколько просили и сколько учеников?

[krem]

Не понравилась цена и количество учеников в классе.

А сколько просили и сколько учеников?

Если мне память не изменяет, то 25-30$ в час, учеников до 16 в классе.

[Murka_]

Дети занимались online и в школе. Online намного практичнее и по уровню учеников/преподавателей выше.

[RrM]

Хмм, я и забыла, что тут - недоговоренное. Sorry. Нет, про BU - ничего не знаю. Скорее всего - добротная стандартная программа, с честным зазубриванием и "покрыванием положенного материала". Как обычно и бывает в университетах с религиозным уклоном.

Хм. Define "систематичный подход". И расскажи, почему он хорош? необходим? Ну в общем, почему ты считаешь "крайнюю несистематичность" заведомо отрицательным качеством?

Мать, слушай, а разве не ты все время подчеркивала, что важна систематичность преподавания математики, а не bag of facts?

Тут две разных эммм... оси имеют место быть. Вполне таких ортогональных. Я потому и попросила - определи, про которую ты речь ведешь. Небось не про ту, которую я имею в виду. Вот и весь парадокс.

1. Преподавание систематичной математики. Математика - это система. Логичная структура, в которой одно вытекает из другого, разные вещи связаны, и бОльшую часть из них - можно вывести из других вещей, и/или они определяются логически (кроме чистых конвенций, типа "что называть целыми числами"). Вот показывать детям эту структуру, ее логику, "big picture" и "что откуда берется" - это и есть то, что я эээ... все время подчеркивала. As opposed to approach "math is a bag of facts" или "bunch of black boxes" - т.е. "понять это невозможно, это можно только запомнить". Когда детей надрессировывают нажимать рычаг, чтобы выпадал банан применять алгоритмы к россыпи (якобы) несвязанных tasks, - и поощряют за каждое "хорошо освоенное знание и умение" типа "щелкни кобылу в нос - она махнет хвостом".

2. Систематичное преподавание математики. Это означает - покрывать все предусмотренные программой темы шаг за шагом, не оставляя 'дырок' и (в случае, например, Кумона) не позволяя ребенку двигаться дальше, пока не покрыто все предыдущее на 100%. As opposed to "двигаться вперед или даже перескакивать, не заботясь о 'покрытии материала', руководствуясь более глобальными соображениями, типа ребенкиного интереса или темы проекта".

[RrM]

Не пойми меня неправильно. Нет, не считаю "сиськемасиськный" подход таким уж необходимым. Сильно талантливый ребенок, аки Ломоносов, сам найдет Периодическую систему среди разрозненных фактов. Впрочем... то, кажется, был не Ломоносов... Не важно.

Это мы про п.1 щас говорим, ага?

Yep. Дети с аналитическим мышлением (не обязательно "сильно талантливые", просто аналитические) автоматом ищут паттерны в окружающем мире и строят mental models и "свертки" как вывести одно из другого. Правда, если он (ребенок) хорошего фидбэка и guidance от взрослых не получает, то может построить неправильные модели, и/или завязнуть в тупике и потратить слишком много усилий. Ну а если окружающие взрослые этого поведения вообще не ценят, а наоборот, ставят хорошие оценки за зубрежку, - то ребенок быстренько отучается от такого неаппрувнутого поведения. Unless он действительно совсем уж математический маньяк талантлив, и делает этот анализ на подсознательном уровне, хоть как его наказывай.

Есть дети, которые "от природы" такого анализа не делают, или делают редко (или которых от этого совсем рано отучили... потому как в общем-то cognitive scientists утверждают, что это делают все поголовно, - мы вообще мир таким макаром осваиваем, только в разных ситуациях применяем в разной степени). Ну скажем так - допустим, есть дети, которые этого не делают (сами по себе, автоматически) для школьной математики. Таким детям - надо эту структуру показывать в явном виде, объяснять explicitly. (первому типу детей - тоже бы желательно, но таки часть из них может перебороть даже и "bag of facts" подход... а вот второй тип - не, не может).

Но сиськемасиськный подход, ты, наверное, согласишься - эффективен, имею в виду получение знания за минимальное (с поправкой на способности ребенка) время.

Если речь идет о п.1 - yep, соглашусь. Как раз именно в математике - в отличие от более "описательных" наук - понимание "откуда что берется" и умение делать "свертки" экономит кучу времени, нервов и энергии. И заодно превентает огромное количество ошибок. Потому как, к примеру, зазубривший "SOHСAHTOA" ученик не имеет никакой возможности проверить логически, правильно ли ему память подсказывает-подсовывает это заклинание, или же правильно будет - "SAHCOHTOA"... да и вообще тратит усилия на лишний шаг в мыслительном процессе - каждый раз, когда ему попадается синус какой-нить.

Если говорить о п.2 - то нет, совершенно и абсолютно не соглашусь. Всяко, конечно, бывает. Но скорее, вообще-то, наоборот. Если занудно прорабатывать весь "положенный материал" и не пущать дальше, пока 100% не выдаст, - КПД будет гораздо ниже, чем если человек станет делать какой-то ему самому интересный проект (пусть даже он только на 80% к нему готов математически) - и в какой-то момент обнаружит, что у него имеется "need to know", и будет мотивирован эти вот недостающие 20% на ходу "подобрать".

Другой разговор, что "преподавать систематично" в смысле п.2 (по кем-то написанной программе/учебнику, покрывать предопределенный "материал", шаг за шагом, отклонение недопустимо) может любой средний добросовестный учитель, даже если сам математики почти не знает (но честно выучил то, что собирается преподавать). А быть гидом-фасилитатором и преподавать по "project-based", "discovery-based" и прочим "active learning" и "student-centered" системам -- это надо на ходу видеть, "чего в супе не хватает", и помогать студенту это осознать, и показывать, где недостающие части искать, - это надо быть на голову выше этого студента. Или лучше - на две головы. Так что КПД-то будет выше, а вот куда кривая дорожка заведет... эт как повезет, на всех-то сильных учителей не хватает же.

[Komissar]

Потому как, к примеру, зазубривший "SOHСAHTOA" ученик не имеет никакой возможности проверить логически, правильно ли ему память подсказывает-подсовывает это заклинание, или же правильно будет - "SAHCOHTOA"... да и вообще тратит усилия на лишний шаг в мыслительном процессе - каждый раз, когда ему попадается синус какой-нить.

мать, дык ведь и синус - косинус это matter of definition. Синус вполне может быть не SOH, a SAH... да, надо запомнить как заклинание. Мятематики столетиями искали зависимость противоположной стороны от угла... из этого и родились со-ка-тоа.

[RrM]

Да, это я неудачный пример выбрала. То есть он хорошо иллюстрирует суб-идею "зазубренные 'факты' - источник ошибок, которые невозможно проверить". Куда я эту иллюстрацию и прилепила.

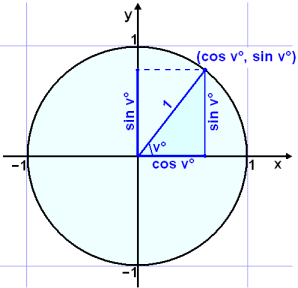
Но он плохо годится для обсуждения основной идеи "логический/сверточный подход делает изучение математики эффективнее". Потому как "синус" и "косинус" - это как раз "конвенции", и названия эти ниоткуда логически не выводяся. И чтобы их не перепутать - надо либо поработать с ними столько, чтоб они осели в подсознание, либо иметь какую-то метафору/прием, чтоб их быстро и достаточно надежно извлечь при надобности. Первое, конечно, было бы лучше, но в реальности - для подавляющего большинства американских школьников синусы-косинусы - это уже "вершина математической пирамиды", так что на оседание надежды практически нету.

Другой разговор, что "треугольная" метафора жутко неудачна сама по себе, как концептуально (привязывает тригонометрию к треугольнику вместо углов), так и практически. В частности - не позволяет орудовать тупыми углами, ващеникак не связана с графиками соответствующих функций (т.е. при чем тут ваще "синусоида" - эт для студента тоже получается black box).

Вполне общепринятая, и логически завязанная на остальную математику (но увы - редко используемая в американской 'school math') метафора или способ определить синусы-косинусы - это unit circle (а уж как запомнить слова, - кто из них синус, а кто - косинус, лучше б каждый студент придумал для себя сам)

[RrM]

Рант про мнемоники. Largely applicable к любому бездумному зазубриванию.

Вообще говоря, любые мнемоники - это лишний слой (или шаг) в ментальном процессе, и как следствие - лишня возможность всадить ошибку. И кроме того - они годятся для "зашифровки" только конкретных имплементаций/рецептов, а не идей и концепций. Т.е. использовать мнемоники для цветов радуги или светимости звезд (чистых словесных конвенций, не завязанных на идеи) - это оправданный прием; использовать же SOHCAHTOA для синусов, PEMDAS для порядка действий или FOIL для перемножения двучленов - это приглашать трабл в будущем. Потому как эти зазубренные слова не дают человеку ничего, кроме зазубренных же "рецептов", че делать в некоторых школьных заданиях, но не дают никакой возможности для понимания концепций и генерализации - "расширения" на соседние (хотя бы) ситуации.

Это еще если в процессе их зазубривания не случилось какого-нибудь квази-логического искажения underlying идей. Человеческие мозги таки стремятся к эффективности и пытаются че-то генерализовать и сделать для себя схемы/модели происходящего. Увы, модели, полученные из мнемоник, эгм... <self-censored>... причем на всю оставшуюся жизнь.

Я в реале общалась со взрослыми людьми (в том числе инженерами), которые на полном серьезе спрашивали "а разве синус - это про угол, а не про треугольник?"; "а разве умножение не делают всегда раньше, чем деление?" и "а разве ваще можно перемножать трехчлены?" (это как раз про три вышеприведенных мнемоники, respectively).

При этом человек, понявший принцип "если действие выше уровнем, его делают раньше" или "каждый член надо умножить на каждый" - не только избегает лишних шагов (mapping мнемонических букв-слов и действий) и непроверяемых ошибок (misremembering как звали тетушку, или какие буквы были в каком порядке). Он еще и совершенно автоматически видит, че получится с тупыми углами, с фигурными скобками или с трехчленами. Если ему придется in real life (или в колледже) столкнуться с не-'schoool-math'.